Context

Concurrency
Parallelism
Distributed Systems

Concurrency

Labeled Transition System (LTS)

A Labeled Transition System (LTS) is a mathematical model used to represent the behavior of concurrent and reactive systems. It’s a formal way to describe how a system moves between different states based on actions or events.

An LTS is formally defined as a tuple: LTS = (S, A, →, s₀)

Where:

S = Set of states
A = Set of action labels (alphabet)
s₀ = Initial state

→ = Transition relation (subset of S × A × S)

Means: “From state s, action a leads to state s’”

Lets draw an example. For that we should declare the rules of the program:

S = {HUNGRY, EATING}
A = {getserving, digest}
s₀ = HUNGRY

Transitions:
HUNGRY --getserving--> EATING
EATING --digest--> HUNGRY

We can now proced with the drawing of the program to visualize its behavior. If done correctly, the drawing should represent exactly the program behavior.

┌─────────┐  getserving  ┌─────────┐
│ HUNGRY  │ ────────────>│ EATING  │
│   s₀    │              │         │
└─────────┘              └─────────┘
      ↑                        │
      │         digest         │
      └────────────────────────┘

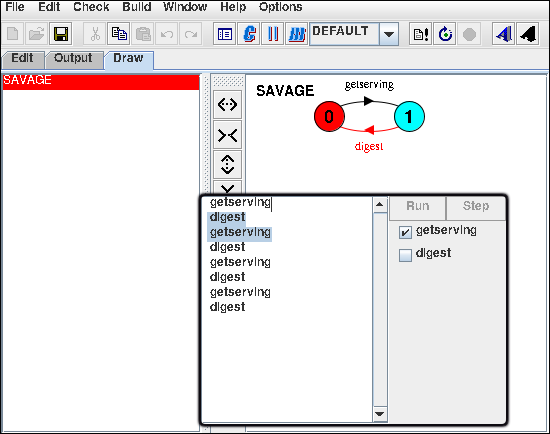
This has been done manually and of course we could make mistakes in the process. For this reason there are tools like LTSA that automate the drawing process based on some “mathematicall notation”. In this course we used FSP notation. It is limited to finite state process and it looks like:

SAVAGE = HUNGRY,
HUNGRY = (getserving -> EATING),
EATING = (digest -> HUNGRY).

LTSA program can then read this notation, draw the program, show alerts such as deadlocks and allow for simple simulations.

FSP Nomenclature

A process is the execution of a sequential program.

PROCESS = STATEMENT1,
STATEMENT1 = (action1 -> STATEMENT2),
STATEMENT2 = (action2 -> STATEMENT3),
STATEMENT3 = (action3 -> END),
END = STOP.

As a process executes, it transforms its states by executing statements.

// Each state (STATEMENT1, STATEMENT2, STATEMENT3) represents a statement being executed.

Each statement consists of a sequence of one or more atomic actions.
```
STATEMENT = (actionA -> actionB -> actionC -> NEXT_STATEMENT).
```
A trace corresponds to an execution of a process.
```
PROCESS = STEP1,
STEP1 = (a -> STEP2),
STEP2 = (b -> STEP3),
STEP3 = (c -> END),
END = STOP.
```
For example, one trace for this process is the sequence of actions:
a->b->c

Other example would be infinit execution with:
```
PROCESS = STEP1,
STEP1 = (a -> STEP2),
STEP2 = (b -> STEP3),
STEP3 = (c -> STEP1).
```
with execution a->b->c->a->b->c->a->b->c->
choice. A process can make a choice between actions. For example, a process that can do either x or y and then return to the starting state:
```
CHOICE = START,
START = (x -> START | y -> START).
```
x->y->x->x->y->x->y->y->y->

Non-deterministic choice: Same action can go to different states.

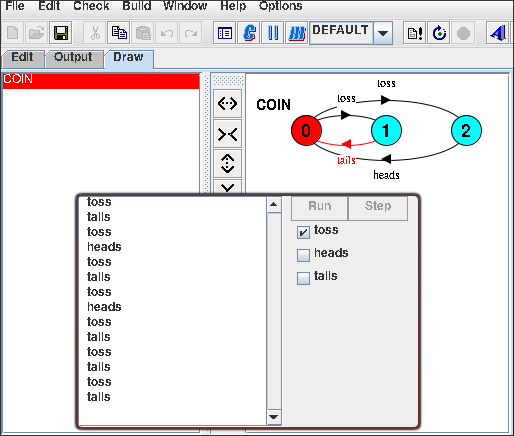
COIN = (toss->HEADS|toss->TAILS),
HEADS= (heads->COIN),
TAILS= (tails->COIN).

unreliable communication channel

CHAN = (in -> CHAN
       |in -> out -> CHAN).

indexed processes and actions: Indexed processes and actions in FSP allow you to define families of actions or processes using indices, making your specifications concise and scalable.
- Short Form: You can use index notation to compactly represent multiple similar actions:
```
BUFF = (in[i:0..3]->out[i]->BUFF).
```
- Long Form
```
BUFF = (in[0]->out[0]->BUFF
    | in[1]->out[1]->BUFF
    | in[2]->out[2]->BUFF
    | in[3]->out[3]->BUFF
).
```
  in[i:0..3] means the action in is indexed from 0 to 3, generating actions in.0, in.1, in.2, in.3. This is useful for modeling buffers, channels, or any structure with repeated, indexed behavior.
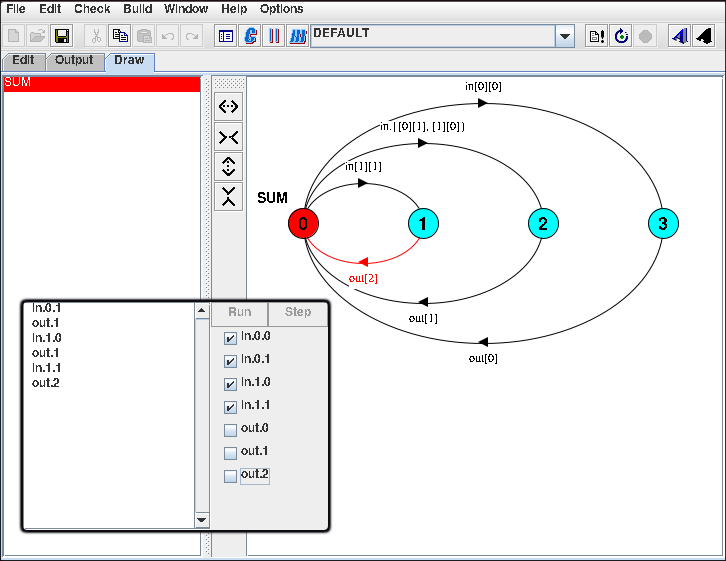
- Using variables for buffer size. You can use constants and ranges to set buffer sizes dynamically:
```
const N = 1
range T = 0..N
range R = 0..2*N
SUM = (in[a:T][b:T]->TOTAL[a+b]),
TOTAL[s:R] = (out[s]->SUM).
```
  Here, N sets the size, and ranges T and R depend on N. This makes your model flexible and easy to scale for different buffer sizes 3.

Process Parameters: in process algebra (like CSP or FSP) are similar to function parameters in programming languages. They allow you to define a process with variables that can be set when the process is instantiated.
- Default Values: In FSP, you typically specify parameters with a range (e.g., i:0..N), but you don’t set default values in the same way as Python. Instead, you set the value when you instantiate the process. For example:
```
BUFF(N=3) = (in[i:0..N]->out[i]-> BUFF).
```
  Here, N is a parameter. When you use BUFF, you provide N:
```
||SYSTEM = BUFF(5)
```
  Process parameters are convenient when:
  - You want to reuse the same process definition with different configurations.
  - You need to model systems with varying sizes or behaviors (e.g., buffer size, number of clients).
guarded actions: we use a while conditional to set the posible actions to take depending on some variable:
```
(when Bx− > P|y− > Q)
```
A simple example is a counter that can not decrease to negative numbers and can not exceed a max value N:
```
  COUNT (N=3) = COUNT[0],
  COUNT[i:0..N] = (when(i<N) inc->COUNT[i+1]
  |when(i>0) dec->COUNT[i-1]
  ).
```
Process naming -> a : P preﬁxes each action label in the alphabet of P with a.
```
SWITCH = (on->off->SWITCH).
||TWO_SWITCH =(a:SWITCH||b:SWITCH).
```

An array of instances of processes:

||SWITCHES(N=3) = (forall[i:1..N] s[i]:SWITCH).
||SWITCHES(N=3) = (s[i:1..N]:SWITCH).

Process labeling Process labeling in FSP allows you to systematically rename actions in a process by adding one or more prefix labels. This is useful for distinguishing actions when composing multiple processes, or when you want to group related actions under a common label.

How Process Labeling Works Suppose you have a process P with actions like n. If you apply a set of prefix labels {𝑎1,…,𝑎𝑥} to P, written as {𝑎1,…,𝑎𝑥}::𝑃, every action n in P is replaced by 𝑎1.𝑛,…,𝑎𝑥.𝑛
```
P = (n -> X).
{a, b}::P
```
This transforms every action n into a.n and b.n, so every transition (n→X) becomes (a.n→X∣b.n→X).
Action relabeling: Relabeling functions are applied to processes to change the names of action labels. The general form of the relabeling function is: /{newlabel_1/oldlabel_1, …newlabel_n/oldlabel_n}
Action hiding: When applied to a process P, the hiding operator {a1, .., ax} removes the action names a1, .., ax from the alphabet of P and makes these concealed actions silent.
- These silent actions are labeled tau.
- Silent actions in different processes are not shared.

Modeling concurrency

As we know, concurrency refers to the ability of a computing system to make progress on multiple tasks during the same time period, allowing different parts of a program to run independently or be interleaved.

We are creating mathematical models to represent a concurrent process (some kind of theoretical implementation) to test if it holds on the real world and point out the possible errors they can throw.

Arbitrary speed: The mathematical model does not know the concept of time, it is abstracted from the design. Therefore we should implement some deleay mechanism to test what happens when actions are executed randomly at time.
Arbitrary relative order of actions from different processes. We call this Interleaving, where a process preserves its own order of actions but they communicate with other processes at any point in time.

This two strategies on an LTS mathematical model offer a general model independent of OS scheduling strategies and asynchronous model of execution.

We will proceed now to show how to implement Arbitrary speed and Arbitrary relative order of actions:

Modeling Parallel Composition / action interleaving

As mentioned above we must design some kind of communication between processes. In FSP we accomplish this with Parallel Composition:

ITCH = (scratch->STOP).
CONVERSE = (think->talk->STOP).
||CONVERSE_ITCH = (ITCH || CONVERSE).

the characters || corresponds to the parallel composition operator. If P and Q are processes then (P||Q) represents the concurrent execution of P and Q.

This processes can now be called on parallel but they are not communicating each other, they are independent. We will talk about shared actions in “Modeling Interaction” chapter.

Modeling Interaction

In concurrent systems, interaction between processes is often modeled using shared actions. When two or more processes have actions with the same label, those actions are considered shared and must occur simultaneously in all participating processes. Unshared actions, on the other hand, can be interleaved arbitrarily.

Example: Maker and User

Consider two processes: a MAKER that manufactures an item and a USER that consumes it. The MAKER signals the item is ready via a shared action ready. The USER can only use the item after receiving this signal.

MAKER = (make -> ready -> MAKER).
USER  = (ready -> use -> USER).
||MAKER_USER = (MAKER || USER).

Here, ready is a shared action. Both processes must synchronize on ready before proceeding. The LTS Analyzer tool can visualize this interaction by composing the processes and drawing the resulting state diagram.

This approach ensures correct coordination between concurrent processes, preventing issues like using an item before it is ready.

Example 1: Handshake

Suppose both the MAKER and USER now synchronize not only on ready, but also on used:

MAKERv2 = (make -> ready -> used -> MAKERv2).
USERv2  = (ready -> use -> used -> USERv2).
||MAKER_USERv2 = (MAKERv2 || USERv2).

Explanation:

Both processes must synchronize on ready as before.
After USERv2 performs use, both must also synchronize on used.
This models a scenario where the item is not only used, but both parties must agree it has been used (e.g., for cleanup or reset).
The system prevents either process from moving past used until both are ready, ensuring tighter coordination.

Example 2: Multi-party synchronization

Now consider a factory with two makers and an assembler:

MAKE_A    = (makeA -> ready -> used -> MAKE_A).
MAKE_B    = (makeB -> ready -> used -> MAKE_B).
ASSEMBLE  = (ready -> assemble -> used -> ASSEMBLE).
||FACTORY = (MAKE_A || MAKE_B || ASSEMBLE).

Explanation:

MAKE_A and MAKE_B each perform their own makeA or makeB actions independently.
All three processes synchronize on ready, meaning assembly cannot start until both makers signal readiness.
ASSEMBLE then performs assemble, while makers wait.
All synchronize on used, indicating the item has been assembled and used, and all can reset.
This models a production line where multiple components must be ready before assembly, and all parties must agree when the product is finished.

Key Principle:
When multiple processes share actions, those actions act as synchronization points. The system enforces that all involved processes must be ready to perform the shared action before any can proceed, ensuring correct sequencing and coordination in concurrent systems.

Handshake: Two-party synchronization
Multi-party synchronization: Three or more processes synchronizing on shared actions

Manual construction of the LTS

Concurrency in Java

Java allows to create concurrent programs when following certain rules. To translate an LTS or FSP programm to a real programming language we will have to make use of some creativity and follow certain rules to make good implementations.

Actions become methods (more or less)